Breadth First Search Algorithm Tutorial with Java
This lesson is part of the course: Artificial Intelligence
Uninformed Search vs Informed / Heuristic Search
The next couple of algorithms we will be covering in this Artificial Intelligence course can be classed as either:
uninformed or blind searches: in which our algorithms have no additional information about states beyond that provided in the problem definition.
Informed or Heuristic searches: in which our algorithms have some extra knowledge about the problem domain and can distinguish whether or not one non-goal state is “more promising” than another.
Breadth First Search
BFS is a simple strategy in which the root node is expanded first, then all the successors of the root node are expanded next, then their successors and so on until the best possible path has been found. Due to the fact that this strategy for graph traversal has no additional information about states beyond that provided in the problem definition, Breadth First Search is classed as an uninformed or blind search.
Breadth First Search Utilizes the queue data structure as opposed to the stack that Depth First Search uses.
BFS uses a queue data structure which is a ‘First in, First Out’ or FIFO data structure. This queue stores all the nodes that we have to explore and each time a node is explored it is added to our set of visited nodes.
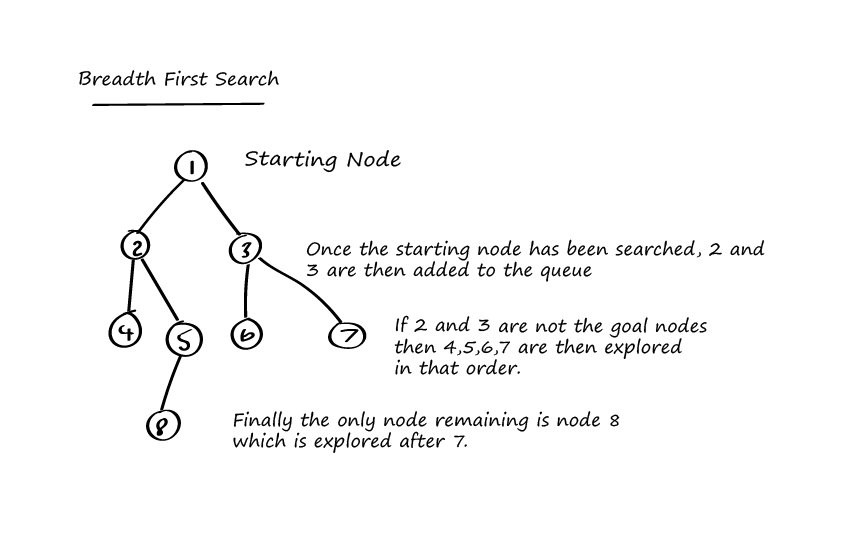
If we were to conduct a breadth first search on the binary tree above then it would do the following:
- Set Node 1 as the start Node
- Add this Node to the Queue
- Add this Node to the visited set
- If this node is our goal node then return true, else add Node 2 and Node 3 to our Queue
- Check Node 2 and if it isn’t add both Node 4 and Node 5 to our Queue.
- Take the next node from our Queue which should be Node 3 and check that.
- If Node 3 isn’t our goal node add Node 6 and Node 7 to our Queue.
- Repeat until goal Node is found.
If we stopped execution after Node 3 was checked then our Queue would look like this:
Node 4, Node 5, Node 7, Node 8.
As you can see, if you follow this algorithm through then you will recursively search every level of the binary tree going deeper and deeper until you find the shortest possible path.
How it Works
Say we had a map of the London Underground, each station would represent a node which would itself have a smaller list of stations that are directly connected to it. The entire map of the London Underground represents our Graph and each of the stations on that graph represent a node.
For example, take Westminster station for example. This station could be represented as a node which would have: STATION 1, STATION 2 and STATION 3 in its list of child nodes.
We can represent this sort of structure like so in Java:
import java.lang.reflect.Array;
import java.util.ArrayList;
/**
* The Node class represents a station
* in this tutorial and will as such have
* a string representing the station's name.
* As well as an ArrayList of nodes that will store
* any instantiated nodes children.
*/
public class Node {
// A Unique Identifier for our node
public String stationName;
// An arraylist containing a list of Nodes that
// This node is directly connected to - It's child nodes.
Node leftChild;
Node rightChild;
public Node(String stationName, Node firstChild, Node secondChild){
this.stationName = stationName;
this.leftChild = firstChild;
this.rightChild = secondChild;
}
public ArrayList<node> getChildren(){
ArrayList<node> childNodes = new ArrayList<>();
if(this.leftChild != null)
{
childNodes.add(leftChild);
}
if(this.rightChild != null) {
childNodes.add(rightChild);
}
return childNodes;
}
// An auxiliary function which allows
// us to remove any child nodes from
// our list of child nodes.
public boolean removeChild(Node n){
return false;
}
}
Our Breadth First Search Class
In this tutorial I will be implementing the breadth first searching algorithm as a class as this makes it far easier to swap in and out different graph traversal algorithms later on.
import java.util.ArrayList;
import java.util.LinkedList;
import java.util.Queue;
/**
* basic breadth first search in java
*/
public class BreadthFirstSearch {
Node startNode;
Node goalNode;
public BreadthFirstSearch(Node start, Node goalNode){
this.startNode = start;
this.goalNode = goalNode;
}
public boolean compute(){
if(this.startNode.equals(goalNode)){
System.out.println("Goal Node Found!");
System.out.println(startNode);
}
Queue<node> queue = new LinkedList<>();
ArrayList<node> explored = new ArrayList<>();
queue.add(this.startNode);
explored.add(startNode);
while(!queue.isEmpty()){
Node current = queue.remove();
if(current.equals(this.goalNode)) {
System.out.println(explored);
return true;
}
else{
if(current.getChildren().isEmpty())
return false;
else
queue.addAll(current.getChildren());
}
explored.add(current);
}
return false;
}
}
The Results
Whilst Breadth First Search can be useful in graph traversal algorithms, one of its flaws is that it finds the shallowest goal node or station which doesn’t necessarily mean it’s the most optimal solution. Breadth First Search is only every optimal if for instance you happen to be in a scenario where all actions have the same cost.
Breadth First graph traversal algorithms also happen to be very computationally demanding in the way that they calculate the shortest path. Take for instance if we have a binary tree of depth 10. The binary tree contains nodes which contain a maximum of 2 child nodes each, this is otherwise known as having a branching factor equal to 2. if we wanted to compute the optimal path for this graph then we would have to traverse, in a worst case scenario, 512 distinct nodes. Given that on modern machines this isn’t exactly what we would consider demanding, imagine if we had a new graph that had 3 child nodes for every node and the same depth of 10. With this new graph we would have to traverse, in a worst case scenario, 19,683 different nodes. And given that this is only at depth 10 with 3 child nodes, you can easily extrapolate the numbers for yourself. With a branching factor of 10 and a depth of 16, it would take 350 years to compute the solution on an ordinary personal computer, give or take.
Our Driver Class
/**
* Our main driver class which instantiates some example nodes
* and then performs the breadth first search upon these newly created
* nodes.
*/
public class Driver {
public static void main(String args[]){
Node station1 = new Node("Westminster", null, null);
Node station2 = new Node("Waterloo", station1, null);
Node station3 = new Node("Trafalgar Square", station1, station2);
Node station4 = new Node("Canary Wharf", station2, station3);
Node station5 = new Node("London Bridge", station4, station3);
Node station6 = new Node("Tottenham Court Road", station5, station4);
BreadthFirstSearch bfs = new BreadthFirstSearch(station6, station1);
if(bfs.compute())
System.out.print("Path Found!");
}
}
Conclusion
If you found this tutorial useful or require further assistance then please let me know in the comments section below!
